我一直有用一个入门款群晖。是单盘位、ARM处理器的那种。上面已经放了一些照片了。随着用的时间越来越久,硬盘的剩余寿命也变得越来越短,导致我的心里越来越慌。再加上最近看了不小捡垃圾组装机器的视频(其实这才是主要原因),我决定组装一个NAS了。
- Nov 30, 2021...more
GitHub Issue 做评论
Oct 3, 2021...more写在前面
我用Hexo生成静态页面,免费部署在Firebase上。本博客就是用这么一个方案服务给读者的。
Hexo 有好多不同风格的主题可以选择。我用的是一个比较大众的主题 apollo 。
我一开始就开启了又 Disqus 提供的评论功能。因为在 Apollo 主题上开启Disqus评论功能很简单,在配置里开启一下就可以了。
但是免费版的 Disqus 评论功能会在评论区域的向下方显示广告。我好久之前就看过朋友的博客用Github Issue当作评论功能来用的方案。假期刚好有时间可以折腾一下博客。所以搜索了一下怎么操作,发现还很好弄的,就整了一个。
Mixin in Java
Feb 28, 2021...moreMixin 指由已有的类功能组合来组装新的类。
Java 自限定类型 (Self-bounded Types)
Feb 27, 2021...more解释了一下自限定类型 (self-bounded types)
消费者/生产者 Java
Feb 12, 2021...more19年面试的时候面试官叫我手写生产者/消费者模型,当时没有写出来。昨天刚好在《Thinking in Java》里看到讲这个,在这分享一下。
显卡安装记
Feb 1, 2021...more坎坷的 RTX 3080 安装过程(翻车现场)
Made a Font, [Katek]
Jun 4, 2018...more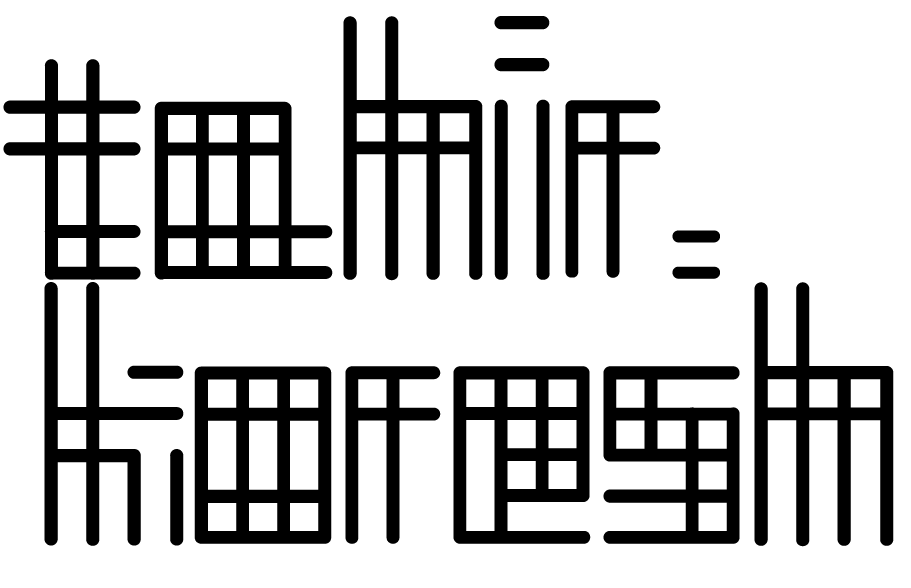
Last week I designed a logo for my blog. I draw my name in the particular form. My colleges suggested me to make a font with it after they saw my logo. Then I tried and made a font.
长沙,第二趟
May 30, 2018...more因为错过航班,出行变的不顺。以这篇日志记录一下这一天。
My first Scheme program
Mar 6, 2018...moreI have started to reading Structure and Interpretation of Computer Programs since last week. And I finished a few exercise of the first chapter. And this is one of them.
厦门旅游记
Feb 20, 2018...more今年公司年会公司带我们去了厦门。